NFA与DFA的转换与优化

March 16, 2014
quote

If it wasn't hard, everyone would do it. It's the hard that makes it great.

— Tom Hanks

上一节《编译原理》课讲到了NFA（不确定的有穷自动机）向DFA（确定的有穷自动机）转换。考试要考，所以要手写变换过程，很繁琐，也很有趣。所以周末用python给实现了，并利用动态规划进行优化。

转换方法

这里主要涉及到对状态集合I的两个操作：

  1. 求ε-闭包。表示为ε-closure(I)，是指I中的任何状态S经过任意条ε弧能到达的状态的集合。
  2. 求I的α弧转换。表示为move(I,α)，是指I中某一状态经过一条α弧到达的状态的集合。

比如说这里有一个NFA N：

NFA

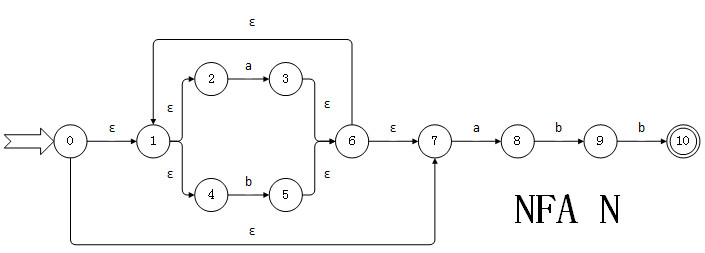
因为NFA是一个五元组，N=(K,E,f,S,Z),即为(状态集合，弧集合，转换集合，开始状态集合，终结状态集合)，所以由图可知：

NFA N = ({0,1,2,3,4,5,6,7,8,9,10},{a,b},f,{0},{10})，其中

  • f(0,ε) = {1}
  • f(1,ε) = {2,4}
  • f(2,a) = {3}
  • f(3,ε) = {6}
  • f(4,b) = {5}
  • f(5,ε) = {6}
  • f(6,ε) = {1,7}
  • f{7,a} = {8}
  • f(8,b) = {9}
  • f(9,b) = {10}

那么ε-closure(0)={0,1,2,4,7}

move({0,1,2,4,7},a) = {3,8}

ε-closure({3,8})={1,2,3,4,6,7,8}

可以借助表格来观察整个求解过程，每次求解后如果产生新集合，就会记录下来继续算，直到没有新集合为止。

T A=ε-closure(move(T,a)) B=ε-closure(move(T,b))
ε-closure(s)={0,1,2,4,7}=T0 {1,2,3,4,6,7,8}=T1 {1,2,4,5,6,7}=T2
T1 T1 {1,2,4,5,6,7,9}=T3
T2 T1 T2
T3 T1 {1,2,4,5,6,7,10}=T4
T4 T1 T2

此时T列下的集合{T0,T1,T2,T3,T4}就是DFA的状态，其中含有NFA初始状态的集合为DFA的初始状态（{T0}），含有NFA终结状态的集合为DFA的终结状态（{T4}）。

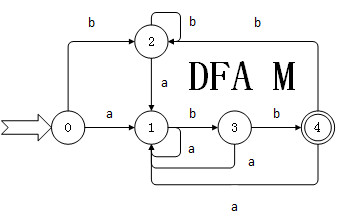
所以由NFA转换后的DFA为：

DFA

实现

首先是数据存储格式，使用json存储NFA的五元组：

{
  "k" : ["0","1","2","3","4","5","6","7","8","9","10"],
  "e" : ["a","b"],
  "f" : {
    "0" : {
      "#" : ["1", "7"]
    },
    "1" : {
      "#" : ["2", "4"]
    },
    "2" : {
      "a" : ["3"]
    },
    "3" : {
      "#" : ["6"]
    },
    "4" : {
      "b" : ["5"]
    },
    "5" : {
      "#" : ["6"]
    },
    "6" : {
      "#" : ["1", "7"]
    },
    "7" : {
      "a" : ["8"]
    },
    "8" : {
      "b" : ["9"]
    },
    "9" : {
      "b" : ["10"]
    }
  },
  "s" : ["0"],
  "z" : ["10"]
}

读入时做了一些简单的判断，其实还可以做得更加周全，比如初始集s和终结集z是否被状态集k包含，等等。read()了之后就会把五元组包装返回。

def read(input):
  try:
    nfa = json.load(open(input,"r"))
    for i in nfa["f"]:
      if not i in nfa["k"]:
        raise Exception("Set f contains iterms that not belongs to set k.")
      for j in nfa["f"][i]:
        if not j in nfa["e"] and not j == '#':
          raise Exception("Set f contains iterms that not belongs to set e.")
    return (set(nfa["k"]), set(nfa["e"]), nfa["f"], set(nfa["s"]), set(nfa["z"]))
  except IOError:
    print "File no found!"
    sys.exit(1)
  except (KeyError, TypeError):
    print "Input data error!"
    sys.exit(1)
  except Exception, e:
    print(e.args[0])
    sys.exit(1)

使用creat_memo()接下来为计算创建缓存，因为计算闭包有大量的重复计算。memo是一个字典，以e集合（弧集合）的元素为键，每一个键对应的值也是一个字典，在计算闭包的过程中缓存该状态的闭包。（见closure()）

def creat_memo(e_set):
  memo = {}
  for i in e_set:
    memo[i] = {}
  memo['#'] = {}
  return memo

从文章开始时提到的转换方法很容易可以看到，两个操作有很大的相似性，所以我把它们封装成一个函数closure()了，调用时使用各自的接口。对应上面提到的弧转换操作，move()中的参数s和arc表示求move(s,arc)，而ph_closure()的arc默认为ε，这里用"#"表示。

def move(f, memo, s, arc):
  return closure(f, memo[arc], s, arc)

def ep_closure(f, memo, s):
  return closure(f, memo["#"], s, '#')

closure()是本程序的核心部分，当它接受了一个集合c_set时，会对c_set中的元素一一进行求闭包或者弧转换，再合并集合。在进行计算之前先查看缓存memo，看看之前有没有计算过，有就直接合并，没有就先计算出结果，在memo记录之后再进行合并。对于求闭包，因为是ε，所以每次要先包含本身，而弧转换则不需要。

注意memo[s] = set([s])，必须是set([s])不能是set(s),因为s为字符串，set(s)会把s中的每个字符都拆开。

接下来判断f转换中是否存在有关f(s,arc)的定义，存在的话：

  1. 闭包情况：深度优先递归的计算集合f(s,arc)的闭包，将它们合并回来。比如上面的NFA例子，一开始求ε-closure(0)的时候，发现f(0,ε)={1,7}，所以继续计算ε-closure(1)和ε-closure(7)。.....一直计算到尽头。每次递归计算过程中也会在memo上记录，所以整个计算过程会越来越快。
  2. 弧转换情况：由于弧只需要判断状态s的下个一个arc弧连接的状态，所以不需要递归，直接得出结果。
def closure(f, memo, c_set, arc):
  res = set()
  for s in c_set:
    if not s in memo:
      memo[s] = set()
      if arc == '#':
        #Attention here. Has to be a list
        memo[s] = set([s])
      if s in f:
        if arc in f[s]:
          if arc == '#':
            memo[s] |= closure(f, memo, set(f[s][arc]), arc)
          else:
            memo[s] = set(f[s][arc])
    res |= memo[s]
  return res

creat_dfa返回一个空的dfa结构，calc_dfa代表了上面提到的表格的运算过程，并把表格的内容保存到dfa结构中。先对初始状态集k求闭包，接下来为每个弧求弧转换闭包ε-closure(move(s, arc))。出现新集合就交给queue队列，并在dfa["k"]中做记录。我这里是利用集合在dfa["k"]中的index作为dfa状态的命名。

def creat_dfa(e_set):
  dfa = {}
  dfa["k"] = []
  dfa["e"] = list(e_set)
  dfa["f"] = {}
  dfa["s"] = []
  dfa["z"] = []
  return dfa

def calc_dfa(k_set, e_set, f, s_set, z_set):
  dfa = creat_dfa(e_set)
  dfa_set = []
  memo = creat_memo(e_set)
  ep = ep_closure(f, memo, s_set)
  #Attention here. Has to be a list
  queue = deque([ep])

  dfa_set.append([ep])
  dfa["k"].append("0")
  dfa["s"].append("0")
  if not len(ep&z_set) == 0:
    dfa["z"].append("0")
  i = 0

  while queue:
    T = queue.popleft()
    j = ""
    index = str(i)
    i = i + 1
    dfa["f"][index] = {}
    for s in e_set:
      t = ep_closure(f, memo, move(f, memo, T, s))
      try:
        j = str(dfa_set.index(t))
      except ValueError:
        queue.append(t)
        j = str(len(dfa_set))
        dfa_set.append(t)
        dfa["k"].append(j)
      dfa["f"][index][s] = j
      if not len(t&s_set) == 0:
        dfa["s"].append(j)
      if not len(t&z_set) == 0:
        dfa["z"].append(j)

  return dfa

生成json的write_dfa和程序的其余代码：

def write_dfa(dfa, f):
  f = open(f, "w")
  f.write(json.dumps(dfa))
  f.close()

def main():
  (k_set, e_set, f, s_set, z_set) = read("NFA.json")
  dfa = calc_dfa(k_set, e_set, f, s_set, z_set)
  write_dfa(dfa, "DFA.json")
  

if __name__ == '__main__'

附上最后生成的json代码，就是上面的图DFA M

{
  "k": ["0", "1", "2", "3", "4"], 
  "z": ["4"], 
  "e": ["a", "b"], 
  "s": ["0"], 
  "f": {
    "1": {
      "a": "1", 
      "b": "3"
    }, 
    "0": {
      "a": "1", 
      "b": "2"
    }, 
    "3": {
      "a": "1", 
      "b": "4"
    }, 
    "2": {
      "a": "1", 
      "b": "2"
    }, 
    "4": {
      "a": "1", 
      "b": "2"
    }
  }
}
NEWER

Jekyll-bootstrap Not Updating Problem Fixed

OLDER

编译原理与计算器

评论没有加载，检查你的局域网

Cannot load comments. Check you network.

eat();

sleep();

code();

repeat();

I code, doodle, tweet & blog.
© COPYRIGHT 2019 · Made With love by CRIMX