编译原理与计算器

March 15, 2014

上次交流会师弟演讲了栈式计算器，这在《数据结构》里也有提到，当时是用C实现了。而这学期学《编译原理》，里面也涉及到数学表达式。两者对比用栈更快，但是使用中间代码可以使到条理更清晰，还可以做很多有趣的扩展。所以这次交流会的内容有着落了。

因为想顺便做个简单的 GUI 看看效果，所以打算用 Qt 或 pyQt，但是之前重装了系统，去下载Qt校园网速又渣渣，最后还是用了 Java。

语法图

先简单的递归定义数学表达式文法，用 EBNF 会比较精炼，但是演讲效果不够图像明显。

表达式：

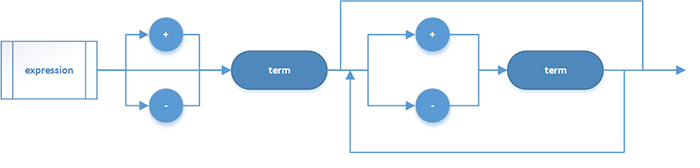
expression

项：

term

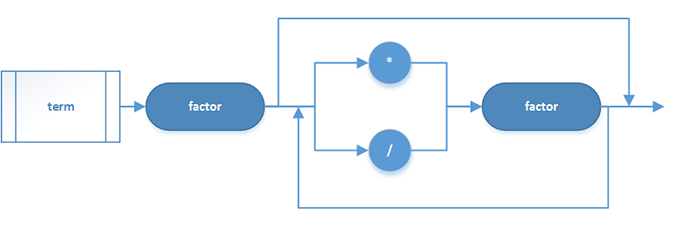
因子：

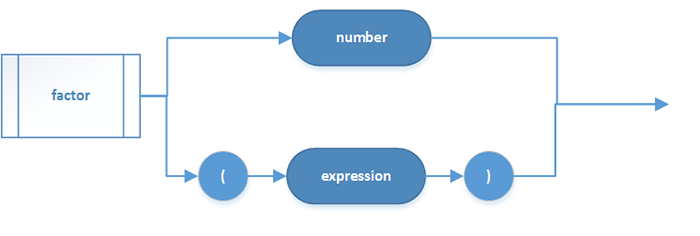
factor

数字

这把所有的数字当做自然数处理：

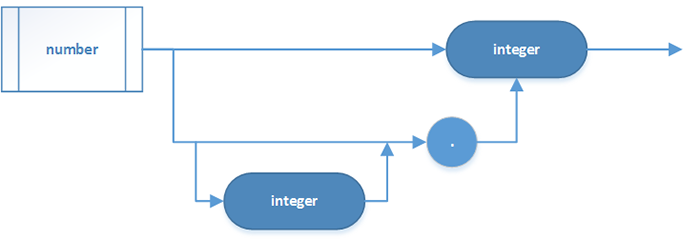
number

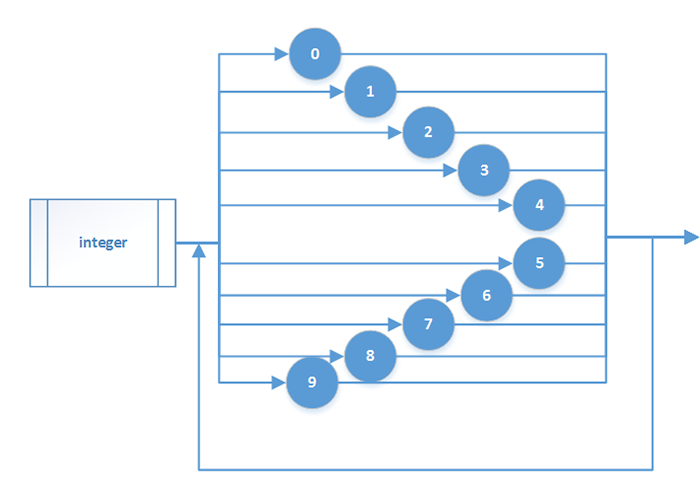
integer

嵌套关系

有了语法图就可以从字符串中把一个个有意义的符号（Token）取出来了。

现在就要关注在上面的语法图中如何嵌套调用去解析一条数学表达式。

比如要解析 25+3/(43-33)-37，如图

nest

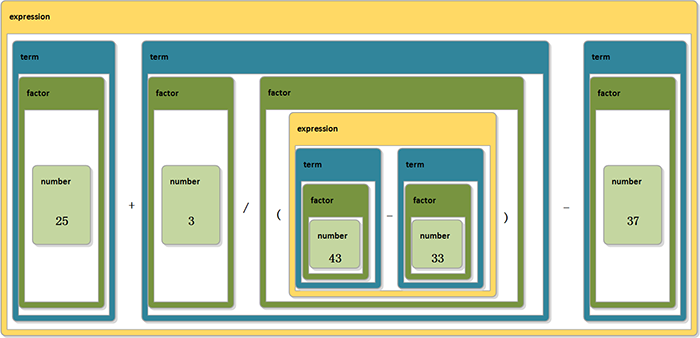
结合之前的语法图会比较好理解，我在PPT上做了动态图。可以看到，每次都从表达式中递归的判断到终结符，扫描一遍就可以建立中间代码了。

中间代码

按照数学运算法则建立中间代码，它是一棵树，叶子结点都是数字，越接近根部的点运算优先级越低。

举例来说，解析 -25+3/(43-33)-(-37) 生成的中间代码如图所示。

ast

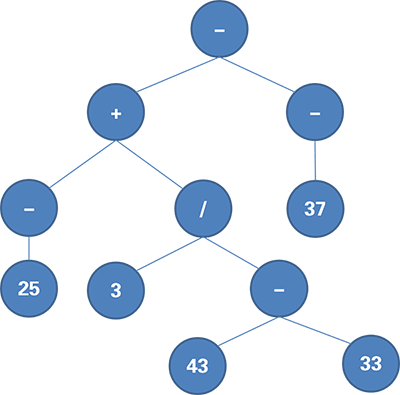
可以结合PPT的动态图理解整个建立过程。扫描的时候，树根为数字遇到操作符便往上方长树，树根为操作符遇到更低优先级的操作符也往上长树，其它情况则往下长。

代码实现

太懒没弄 UML 图，不过类也不多，直接讲吧，完整源码在这里。

首先是 Token 类，扫描时就会将字符串生成一个个 Token。

private TokenType type; // 该token的类型
private double number;  // 数字
private String op;      // 操作符

我这里是图省事把 Token 也当做中间代码的结点，所以里面还实现树相关的属性和方法，为中间代码的结点单独设计类会更好。

private ArrayList<Token> children = null; // 孩子

public void addChild(Token token){/*......*/}

接下来看 TokenType 类，这里枚举了所有可能的类型。

public enum TokenType {
  
  //数字
  NUMBER,
  
  //操作符
  PLUS, MINUS, STAR, SLASH,
  LEFT_PAREN, RIGHT_PAREN,
    
  //负数
  NEGATE,
  
  //结束
  EOF;
}

有了 Token 和 TokenType，Scanner 类负责扫描一遍表达式并提取一个个 Token。因为这里的符号（Token）只有数字与负号（见上面的 TokenType），所以判断起来并不复杂，注意一下处理小数点。

// 数字处理
if(Character.isDigit(currentChar) || currentChar == '.') {
  return extractNumber();
}
else {
  nextChar(); // 先消耗掉这个字符
    switch(currentChar) {
    case '+': return new Token(PLUS, '+'); 
    case '-': return new Token(MINUS, '-'); 
    case '*': return new Token(STAR, '*');
    case '/': return new Token(SLASH, '/'); 
    case '(': return new Token(LEFT_PAREN, '('); 
    case ')': return new Token(RIGHT_PAREN, ')');  
    case (char)0:return new Token(EOF); 
    default : throw new Exception("有未识别的字符 \""+ currentChar + "\" !");
  }
}

Parser 类就完全是对应着上面的语法图去实现了，遇到非终结符便递归，逻辑非常清晰，可以参看源码

生成中间代码后，在后端实现一个 Calculator 去计算中间代码，更加简单，自上往下递归计算即可。

private double calculate(Token token) throws Exception {
  
  if(token != null) {
    ArrayList<Token> children = token.getChildren();
    if(children == null) {
      return token.getNumber();
    }
    else {
      switch(token.getType()) {
      case PLUS   : return calculate(children.get(0)) + calculate(children.get(1));
      case MINUS  : return calculate(children.get(0)) - calculate(children.get(1));
      case STAR   : return calculate(children.get(0)) * calculate(children.get(1));
      case SLASH  : return calculate(children.get(0)) / calculate(children.get(1));
      case NEGATE : return -1 * calculate(children.get(0));
      default     : throw new Exception("计算出错！" + token.getType().toString());
      }
    }
  }
  return 0;
}

就这样表达式计算就完成了。用 CalcMachine 类测试效果。

其中使用正则表达式隐藏异常中不必要的信息。

Pattern.compile("^.*Exception:").matcher(e1.toString()).replaceAll("")

总结

希望大家读完这篇文章后：

学会了理解语法图
学会了简单的词法分析和语法分析
使用递归可以十分灵活、方便
计算器的功能很容易扩展
功能分块可单独测试，便于查错、维护，特别是对于此类逻辑复杂的系统

#编译原理 #Compiler

NEWER

NFA与DFA的转换与优化

评论没有加载，检查你的局域网

Cannot load comments. Check you network.